§1. Введение в релевантную геометрию
Определение. Релевантным базисом (Ϟ-базисом) в пространстве будем называть три геометрических вектора a_Ϟ, b_Ϟ, c_Ϟ, удовлетворяющих следующим условиям-аксиомам:
1. a_Ϟ ⊥ b_Ϟ, b_Ϟ ⊥ c_Ϟ, a_Ϟ ⊥ c_Ϟ
2. |a_Ϟ| = |b_Ϟ| = |c_Ϟ| = Ϟ → 0
3. V = V_a · a_Ϟ + V_b · b_Ϟ + V_c · c_Ϟ => {V_a, V_b, V_c} ⊂ Z
4. V = V_a · a_Ϟ + V_b · b_Ϟ + V_c · c_Ϟ => |V|_Ϟ = Ϟ · (|V_a| + |V_b| + |V_c|) = |Пр_aϞV| + |Пр_bϞV| + |Пр_cϞV| (релевантная длина вектора)
Релевантный базис на плоскости будем определять аналогичным образом.

Замечание. Векторы релевантного базиса будем обозначать в дальнейшем через i_Ϟ, j_Ϟ, k_Ϟ. Если V = V_i · i_Ϟ + V_j · j_Ϟ + V_k · k_Ϟ, то числа V_i, V_j и V_k будем называть бесконечными координатами вектора V относительно релевантного базиса i_Ϟ, j_Ϟ, k_Ϟ, а числа x_Ϟ = Ϟ · V_i, y_Ϟ = Ϟ · V_j, z_Ϟ = Ϟ · V_k - конечными координатами вектора V.
Релевантную длину любого вектора можно выразить через его конечные координаты следующим образом: |V|_Ϟ = |x_Ϟ| + |y_Ϟ| + |z_Ϟ|.

Определение. Под релевантной системой координат в пространстве будем понимать систему координат, определяемую заданием релевантного базиса - трёх векторов i_Ϟ, j_Ϟ, k_Ϟ, для которых выполняются перечисленные выше условия-аксиомы, и некоторой точки O - точки приложения векторов релевантного базиса.
Под релевантными координатами произвольной точки M пространства будем понимать координаты вектора OM относительно релевантного базиса i_Ϟ, j_Ϟ, k_Ϟ.
Дискретными осями Ox_Ϟ, Oy_Ϟ и Oz_Ϟ будем называть три луча, исходящих из точки O параллельно векторам i_Ϟ, j_Ϟ, k_Ϟ соответственно.
Релевантную систему координат на плоскости будем определять аналогичным образом.

Прежде всего выведем формулу, связывающую обычную, "действительную", нерелевантную длину вектора, не зависящую от выбора системы координат, с его релевантной длиной на плоскости.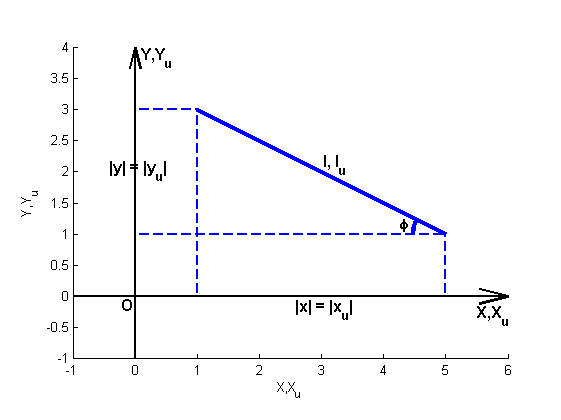Пусть некоторый вектор имеет релевантную длину l_Ϟ и нерелевантную длину l, его конечные координаты равны x = x_Ϟ и y = y_Ϟ и образует с одной из релевантных осей угол Φ.
Квадрат его нерелевантной длины можно вычислить по формуле: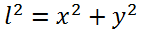Из формулы же для его релевантной длины получаем: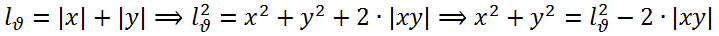Из образовавшегося на рисунке прямоугольного треугольника несложно найти, что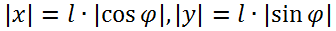Таким образом, компонуя все приведённые выше формулы и учитывая формулу синуса двойного угла, приходим к конечной формуле: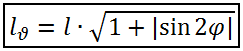Аналогичными рассуждениями можно прийти к формуле, связывающей релевантную и нерелевантную длины любого вектора в пространстве. Пусть cos α, cos β и cos γ - его направляющие косинусы, тогда формула примет вид: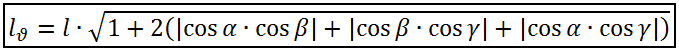

Замечание. Во-первых, из выведенной нами формулы вытекает, что на плоскости релевантная длина любого вектора не меньше его нерелевантной длины: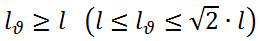Во-вторых, несложно заметить, что углом Φ в формуле, связывающей релевантную и нерелевантную длины вектора, может являться любой из углов (как острый, так и тупой) между вектором и одной из релевантных осей (как Ox_Ϟ, так и Oy_Ϟ).